2023/02/24 | 社員ブログ

こんにちは。私は豊和開発株式会社の設計監理部で意匠設計、設計監理を担当している小浦です。前回、杭工事のために土を掘る話をしました。今回は土を掘ったその後、杭打ちについて話をしたいと思います。
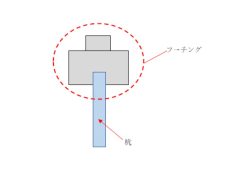
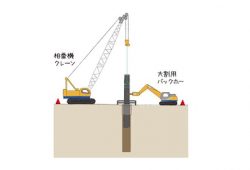
杭打ちの為、土を掘った後、大きな丸い穴が開いています。この穴にコンクリートを流し込むと杭になりますが、ただ流し込むだけではありません。杭が地中で柱として成り立つためには、コンクリートの中に鉄筋が必要です。土の中では、様々な方向から杭に力が加わるので、この鉄筋がなければ杭が折れてしまいます。鉄筋は人間でいえば骨と同じです。骨がなければ人は真っ直ぐに立てないのと同じで、鉄筋がないと杭は地中で折れてしまい、建物を支えることができなくなり、結果建物は傾いてしまいます。それを防ぐ為に、土を掘った後、コンクリートを流し込む前に初めに鉄筋を入れるのです。その鉄筋は穴の直上から差し込んでいきます。丸い穴の中に地上で組みあがった鉄筋をクレーンで入れるわけです。その鉄筋は上から見ると穴に沿うような円の形をしています。
杭穴に差し入れる鉄筋は地上で組み立てられます。杭は円柱形なので、横向きの鉄筋は、丸い形をしています。丸い鉄筋を所定本数の縦向きの鉄筋で組み上げます。この円柱形に組まれた鉄筋を鉄筋かごといいます。鉄筋を結束して作られる為名前通り、鉄でできた籠のように見えます。数十メートルも掘削を行う場所打ち杭では、実際に地面深くまで潜って鉄筋を組み立てるのは難しいので、予め地上で必要な鉄筋を組み立てておく必要があります。組み上げられた円柱形の鉄筋を穴の直上に吊り下げ、穴の側面に接触しないように、穴が崩れてしまわないよう慎重に下ろしていきます。支持杭という杭先端が地球の固い部分の地盤で支持するものの場合、杭の穴は時に何十メートルもの深さになることがあります。しかし、鉄筋かごはトラックで運ぶことのできる長さの限界があり、限界以上の長さの杭を作る為には、複数の鉄筋かごを途中で繋ぐ必要があります。1本目の鉄筋かごを途中で止めて1本目の上部と2本目の下部とを繋ぎます。鉄筋と鉄筋をつなぐ方法としては、針金(結束線)で結束する。溶接する。ボルトで固定する等方法は色々ありますが、その時々の現場の状況に合わせて方法は決められます。

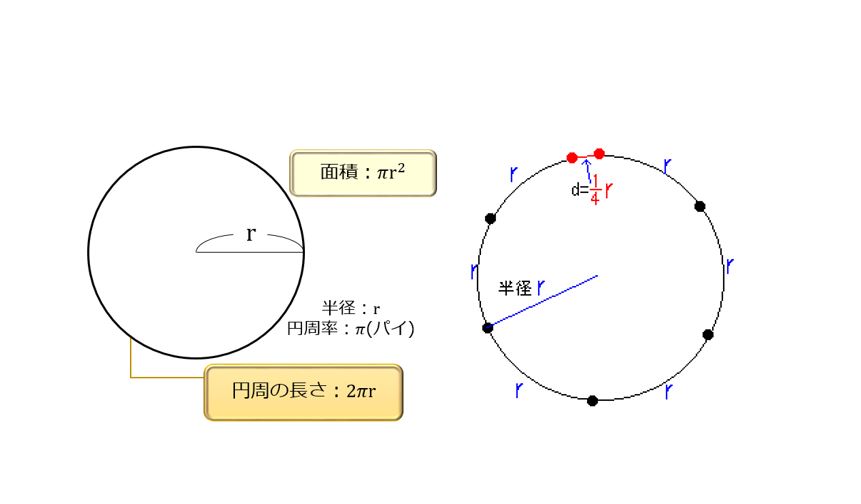
鉄筋を入れた後、コンクリートを流し込むわけですが、流し込む量の計算にも一苦労があります。杭穴の大きさとと深さでコンクリートの体積が割り出せます。体積は円の面積と長さで求められます。円の面積の計算には小学校で習った円周率π=3.14が使われます。円周率π=3.141592653589 793238462643・・・・、 円周率はどこまでも続く数字で10万桁以上も覚えた日本人の方もいるそうですが、残念ながらギネス記録には認定されていません。(ちなみにギネス記録は7万桁 でインド人の方が保持されています。さすが数学の国。)聞くところによると今の小学生は円周率π=3で計算する事もあるらしいですが、図面上で杭の直径2mの場合が半径が1mとなる。この時の円の面積は円周率π=3.14を使うと3.14m2となる。円周率π=3で計算すると3.00m2となる。円周率π=3として計算すると、求められる体積はかなり小さくなってしまいます。仮に、杭の深さが20mとすると体積の差は2.8m3となってしまいます。このように円周率π=3で計算すると大変な誤差が生じるので、業務では円周率π=3の値は使わず、円周率π=3.14で計算を行っています。円の面積は半径×半径×円周率π3.14で割り出す事ができます。
余談ですが、ここで大昔に使われていた円周率の計算方法についてお話します。古代にはコンパスや正確な定規などありませんでしたが、1本の糸と木切れを使うだけで、現在の円周率に近しい数値を割り出す事ができました。まず糸の両面に木切れをくくりつけて地面に円を描き,その糸をそのまま定規の代わりにして円に沿って、円周を測っていきます。すると糸6本分と少しが余ります。そこでこの糸を四つ折りにして余った長さにあててみると,かなり近い事がわかります。円周を L,半径を r,余りの長さを a とするとL=6r+aとなります。dは半径の1/4に近いので,a≒r/4 となります。L ≒ 6r+1/4r=2(3+1/8)rとなって円周を求める式は,L=2πrだからπ≒3+1/8=3.125 となります。現在のπは3.14なのでおおよそ同じです。木切れと糸だけでも,これだけ正確に測ることができるのできたのです。ちなみにこの円周率の求め方は,バビロニア(メソポタミアの古代都市)で使われていたもので、エジプト、黄河、インダスと並び世界四大文明の一つで最古の文明であるメソポタミアです。紀元前9千年に遡る歴史を持ち、古代文明発祥の地です。この時代にすでに ほぼ現在の円周率に近しい数値を割り出すことができていたなんて、古代人はすごいと思います。以上、木切れと糸があれば出来る、円周率の割り出し方のお話でした。
ここからは杭打ちでコンクリートを流し込む際の話に戻ります。円の面積×深さ=杭の穴の体積が割り出され、コンクリートを発注できるかと思いきや、まだ、計算すべき事があります。図面の杭穴の直径が1mの場合、実際の掘った穴はそれよりも少し大きくなってしまいます。穴を掘るドリルの直径が1mの場合、回しながら掘るドリルを引き抜いた時、若干穴は大きくなります。それに付け加え地中には、石・砂・粘土が混在している為、杭穴の途中で砂が崩れてしまったり、杭穴の途中に石が取れた穴があるかもしれません。コンクリートの流し込み量も、図面上よりも、少し多くなります。それを見越してコンクリートの量を計算しなければなりません。そしてコンクリートを運んでくる車はミキサー車です。大型のミキサー車は4.5㎥のコンクリートを運ぶことができます。コンクリートの量÷4.5㎥でミキサー車の台数が決まるのです。コンクリートの量が4.5㎥の倍数なら、ちょうど整数の台数になりますが、そうはうまくいかないのが現場の常です。また、コンクリート工場から現場まで運ぶのには、勿論時間がかかります。コンクリートの発注に無駄が無いよう、コンクリートを流し込んでから最後の端数分を手配するのでは時間のロスがあります。事前に最後のミキサー車でコンクリートの量を調整し、ほぼぴったりとなるよう手配するのが現場での腕の見せ所といえるでしょう。

杭の為の穴にコンクリートを流し込む量は、掘る量と同様に図面の数値とは違うということを考えて計算しなければなりません。ここでも各建設現場ごとにその時の地盤の状況で、図面上では同じ杭でも、掘った穴ごとに流し込むコンクリートの量は変わってきます。固い地質と柔らかい地質によっても土の崩れ方が変わるので、コンクリートの量の計算も自然との闘いになるわけです。建築とはまさに自然を考え、その時々の状況を考えなければなりません。単なる計算だけではなく、経験と知識が必要になってきます。ここでも数字での戦いがあります。答えの無い戦いだからこそ、建築をしていると自然が好きになり数字が好きになり計算が好きになっていきます。
今後も、そんな自然と数字に関わる話をさせて頂けたらと思います。
最後までお読み頂きありがとうございました。


 社員ブログ
社員ブログ
建物を建てる際、最も重要な手続きの一つが「確認申請」です。建築主や設計者が
 社員ブログ
社員ブログ
みなさん、ご無沙汰しております。
豊和開発株式会社【営業本部】
 社員ブログ
社員ブログ
今回は、2025年に大阪・関西で開催され、半年間にわたり多くの人々の注目を
 社員ブログ
社員ブログ
土地を所有している人にとって、共通の悩みのひとつが「どう活用すべきか」とい
 社員ブログ
社員ブログ
建築管理部の沖見です。
今回は、私の所属部署である「建築管理部
 社員ブログ
社員ブログ
20年以上昔の話ですが、友人(大阪府在住)から「T県のS市(所要都市)の駅
 社員ブログ
社員ブログ
こんにちは。中途採用にて入社いたしました、総務担当の原島です。
 社員ブログ
社員ブログ
建築とは、単なる空間の構築ではありません。
そこには時代の思想
 社員ブログ
社員ブログ
豊和開発株式会社 経営企画部の山田と申します。
デジタル変革(
 社員ブログ
社員ブログ
皆様、いつも有難うご ざいます。 私は豊和開発株式会社の香川清和と申します
 社員ブログ
社員ブログ
こんにちは、豊和開発株式会社で主に経理を担当しています村上です。
 社員ブログ
社員ブログ
土地所有者様が土地活用の一環として、介護・保育・医療等の施設を建てるメリ
 社員ブログ
社員ブログ
社員を採用した際、また退職した際、それに月々の給与計算など、社会保険にまつ
 社員ブログ
社員ブログ
地球温暖化やエネルギー資源の減少や枯渇といった課題が、かつてないほど私たち
 社員ブログ
社員ブログ
皆さま、お世話になっております。豊和開発株式会社入社2年目の神谷昊輝(かみ
 社員ブログ
社員ブログ
皆さんお久しぶりです。営業本部の坪田です。
今回は日本の少子高
 社員ブログ
社員ブログ
私は、豊和開発(株)の設計監理部で日々建築設計業務に従事しています。
 社員ブログ
社員ブログ
エジプトのギザにはピラミッドが建っています。
教科書やテレビで
 社員ブログ
社員ブログ
「これ、本当に建物に使えるのかな?」
近年、建築現場で次々と登
 社員ブログ
社員ブログ
今年の4月より中途採用にて入社致しました社員Mと申します。
 社員ブログ
社員ブログ
皆さま、はじめまして。
私は2025年春に新卒で入社し、現在、
 社員ブログ
社員ブログ
4月から豊和開発の設計監理部に新入社員として入社しました。
設
 社員ブログ
社員ブログ
都市部における土地利用を効率的かつ正しく行うために、さまざまな法的な規制が
 社員ブログ
社員ブログ
豊和開発では毎年多くの建物を建築しておりますが、近年の傾向を見ると半数以上
 社員ブログ
社員ブログ
消費税の区分として「課税」「不課税」「非課税」「免税」がありますが、このう
 社員ブログ
社員ブログ
「古墳」・・・太古の地域権力者のお墓。
関西では奈良県はもとよ
 社員ブログ
社員ブログ
私は豊和開発株式会社の設計監理部の一員としてがんばっております。今回は仕事
 社員ブログ
社員ブログ
こんにちは、豊和開発株式会社で主に経理を担当しています村上です。
 社員ブログ
社員ブログ
昨今の日本では所有者不明の土地が問題になっております。調査を尽くしても土地
 社員ブログ
社員ブログ
こんにちは、豊和開発で人材採用を担当している本田と申します。
 社員ブログ
社員ブログ
こんにちは,豊和開発株式会社 営業の橋本隆行と申します。当社は、土地オーナ
 社員ブログ
社員ブログ
近年、3Dプリンター技術が建築業界に変革をもたらすと注目されています。従来
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社 営業本部の荒木と申します。
弊
 社員ブログ
社員ブログ
お世話になっております。豊和開発株式会社2年目の神谷です。
土
 社員ブログ
社員ブログ
皆様こんにちは。豊和開発株式会社営業本部の坪田です。
今回の
 社員ブログ
社員ブログ
豊和開発では新築の建物を設計する事がほとんどです。建物をお施主様にお引渡し
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社のKと申します。私は現在経営企画部という部署で
 社員ブログ
社員ブログ
近年、カーボンニュートラルや温室効果ガス排出削減の実現など、地球環境の保全
 社員ブログ
社員ブログ
皆さんは建築施工管理業務はご存じですか?
我々豊和開発では、
 社員ブログ
社員ブログ
日本の高齢化が深刻化していく中で、介護を必要とする高齢者が増加しており、そ
 社員ブログ
社員ブログ
こんにちは。建築管理部の沖見です。
2022年11月からご紹
 社員ブログ
社員ブログ
経理業務における重要業務のひとつである「決算」。
経理にとって
 社員ブログ
社員ブログ
1991年にこのタイトルで公開された織田裕二さん主演の映画が製作されたころ
 社員ブログ
社員ブログ
最近、とても寒い日々が続いています。外に出ると風も冷たく、暖かい部屋が恋し
 社員ブログ
社員ブログ
豊和開発で意匠設計を担当しています新本と申します。
就活や転
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社 経営企画部の村上です。私は、部内で主に経理を
 社員ブログ
社員ブログ
私、豊和開発の営業の橋本と申します。今回は、土地活用での個人事業主様の所得
 社員ブログ
社員ブログ
土地活用とは、言葉の意味を表現すると土地を活かして用いるとなります。現状(
 社員ブログ
社員ブログ
こんにちは、豊和開発の営業マン、段原です。
不動産にかかる税金
 社員ブログ
社員ブログ
こんにちは、豊和開発株式会社、設計監理部の上川です。私は4月に新卒入社して
 社員ブログ
社員ブログ
こんにちは。営業本部の荒木です。4月に入社して早くも8か月が経ち、年の終わ
 社員ブログ
社員ブログ
皆さんは社会人として必要不可欠である「報連相(ほうれんそう)」をしっかり理
 社員ブログ
社員ブログ
お久しぶりです、豊和開発営業本部の坪田です。
今回のコラムでは
 社員ブログ
社員ブログ
豊和開発株式会社設計監理部で建物の意匠設計業務を担当させて頂いております。
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社のKと申します。
私は大学を卒業し
 社員ブログ
社員ブログ
先日、2024年10月13日(日)に一級建築士の製図試験が行われました。受
 社員ブログ
社員ブログ
当社では当社が建築に携わった施設はもちろん、既存の建物につきましても、オー
 社員ブログ
社員ブログ
豊和開発で経営企画部という部署で採用担当をしている久保です。
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社 営業本部の下元です。
私は主に、
 社員ブログ
社員ブログ
こんにちは。建築管理部の沖見です。
2022年11月からご紹介
 社員ブログ
社員ブログ
今春、全国12都県で約100施設の障がい者グループホームの運営をしている、
 社員ブログ
社員ブログ
豊和開発株式会社で経理を担当している木村と申します。
弊社では
 社員ブログ
社員ブログ
こんにちは。私は豊和開発株式会社の設計監理部で意匠設計、設計監理を担当して
 社員ブログ
社員ブログ
こんにちは。経営企画部の村上です。私は、部内で主に経理を担当しております。
 社員ブログ
社員ブログ
こんにちは。営業本部の佐竹です。
仕事柄、土地活用の提案をし
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社 営業本部の段原です!
私は今年
 社員ブログ
社員ブログ
はじめまして、2024年4月に新卒入社致しました、豊和開発株式会社、設計監
 社員ブログ
社員ブログ
はじめまして。2024年4月より豊和開発に入社いたしました、営業本部の荒木
 社員ブログ
社員ブログ
こんにちは!豊和開発株式会社 営業本部の神谷です!
私は数ヶ
 社員ブログ
社員ブログ
皆さんこんにちは。豊和開発営業本部の坪田です。
今回のコラムで
 社員ブログ
社員ブログ
豊和開発株式会社設計監理部の大谷です。
土地をお持ちの方でそ
 社員ブログ
社員ブログ
こんにちは。豊和開発の経営企画部のKと申します。
夜にスマート
 社員ブログ
社員ブログ
こんにちは。豊和開発の営業マン、黒田です。
社会人であれば、見
 社員ブログ
社員ブログ
現在、世界的な「脱炭素社会の進展・カーボンニュートラル達成」を目指す動きが
 社員ブログ
社員ブログ
こんにちは。豊和開発のTです。私たちの生活の中に当たり前のように存在してい
 社員ブログ
社員ブログ
設計監理部の山本です。今回は開催がちょうどあと一年に迫った世間を騒がしてい
 社員ブログ
社員ブログ
本来は、資産として捉えられるべき物件の中には、不動産ならぬ負動産と呼ばれて
 社員ブログ
社員ブログ
初めまして、もうすぐ中途入社して半年が経つ豊和開発で経理を担当しております
 社員ブログ
社員ブログ
豊和開発で経理を担当しております木村と申します。
今回の定額減
 社員ブログ
社員ブログ
こんにちは。建築管理部の沖見です。
堺市で建築した鉄骨造の老人
 社員ブログ
社員ブログ
今年は、コロナ明け初の「お花見」シーズンという事で、大きな経済効果が期待さ
 社員ブログ
社員ブログ
こんにちは。私は豊和開発株式会社の設計監理部で意匠設計、設計監理を担当して
 社員ブログ
社員ブログ
こんにちは。営業本部の佐竹です。過去3回地鎮祭についてのコラムを書いてきま
 社員ブログ
社員ブログ
 社員ブログ
社員ブログ
こんにちは。経営企画部の岩村です。私は普段、新卒採用や教育など、人事業務に
 社員ブログ
社員ブログ
土地活用といっても、土地の立地や大きさなどの条件やどういったもので活用する
 社員ブログ
社員ブログ
建築設計をする上で欠かせないものの一つにライティングプラン があります。建
 社員ブログ
社員ブログ
この度は豊和開発株式会社では、フリーアナウンサーである森たけし氏就活セミナ
 社員ブログ
社員ブログ
こんにちは。昨年の11月に豊和開発株式会社へ中途入社しました、経営企画部の
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社の設計監理部に在籍しているTです。
 社員ブログ
社員ブログ
こんにちは。営業部の黒田です。私は2020年4月に入社し、もうすぐ丸4年が
 社員ブログ
社員ブログ
過去の投稿(2023年10月6日 投稿)では建築管理部が行う「安全管理」業
 社員ブログ
社員ブログ
豊和開発株式会社 久保です。前回に引き続き2023
 社員ブログ
社員ブログ
あけましておめでとうございます。設計監理部の山本と申します。
 社員ブログ
社員ブログ
今回は「地中障害物」について解説いたします。
まず地中障害物と
 社員ブログ
社員ブログ
こんにちは。建築管理部の沖見です。
今回も、引き続き、堺市で建
 社員ブログ
社員ブログ
この2年位、当社を志望する就活生の前で、豊和開発の営業の仕事について、お
 社員ブログ
社員ブログ
豊和開発営業本部の山本です。建物の建ぺい率と容積率は、暮らしやすい環境を維
 社員ブログ
社員ブログ
こんにちは、私は豊和開発の設計監理部にて福祉施設の設計監理業務に携わってお
 社員ブログ
社員ブログ
こんにちは。営業本部の宮と申します。土地オーナ様に土地活用の提案をさせて
 社員ブログ
社員ブログ
こんにちは。私は豊和開発株式会社の設計監理部で意匠設計、設計監理を担当して
 社員ブログ
社員ブログ
こんにちは。営業本部の佐竹と申します。前々回、前回のコラムでは、地鎮祭の事
 社員ブログ
社員ブログ
こんにちは!豊和開発株式会社 経営企画部 岩村です。
私は普段
 社員ブログ
社員ブログ
豊和開発株式会社に入社し5年目になりますが、何件かの認可保育所の設計に携わ
 社員ブログ
社員ブログ
豊和開発株式会社 営業本部営業課の坪田です。
今回のコラムでは
 社員ブログ
社員ブログ
豊和開発経営企画部の久保です。経営企画部では、採用・教育・総務・経理等の幅
 社員ブログ
社員ブログ
こんにちは。日々、仕事ができる人と、できない人の違いは何かと考えている、新
 社員ブログ
社員ブログ
こんにちは。私は、今年新卒で入社いたしました設計監理部 山本と申します。豊
 社員ブログ
社員ブログ
過去の投稿(2023年6月9日 投稿)では建築管理部が行う安全管理業務の内
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社採用担当の村井です。本日は新卒の就職活動期間に
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社 営業本部の下元です。今回のコラムは「住宅型有
 社員ブログ
社員ブログ
こんにちは。建築管理部の沖見です。
今回も、引き続き、堺市で建
 社員ブログ
社員ブログ
豊和開発で土地有効活用の営業をしている田宮です。今年からインターンシップの
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社の営業本部に所属している山本と申します。
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社営業本部所属の石垣と申します。
 社員ブログ
社員ブログ
豊和開発株式会社設計監理部に所属している長浜と申します。
設計
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社の宮と申します。弊社は、土地の有効活用提案を
 社員ブログ
社員ブログ
こんにちは。私は豊和開発株式会社の設計監理部で意匠設計、設計監理を担当して
 社員ブログ
社員ブログ
こんにちは。営業本部の佐竹と申します。
前回のコラムでは地鎮
 社員ブログ
社員ブログ
こんにちは、経営企画部の岩村です。
私は普段、採用業務を担当し
 社員ブログ
社員ブログ
みなさんお久しぶりです。営業本部の坪田です。
今回のコラムは少
 社員ブログ
社員ブログ
弊社設計監理部では主に老人介護施設や保育所といった社会福祉施設の設計・監理
 社員ブログ
社員ブログ
こんにちは。私は新卒社員で入社し、現在4年目の営業マン、黒田です。私共、豊
 社員ブログ
社員ブログ
建築管理部の小早川です。
過去の投稿(2022年12月16日
 社員ブログ
社員ブログ
豊和開発株式会社 久保です。私は、当社の経営企画部で、総務の仕事とともに、
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社 営業本部 山下と申します。私は、貿易業界から
 社員ブログ
社員ブログ
家の近所を歩いていてふと上空を見上げると高圧線が目に入ることがあり、高圧線
 社員ブログ
社員ブログ
こんにちは。経営企画部の村井です。
今回知ってほしい内容は『コ
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社 営業本部の下元です。今回のコラムは「駅から遠
 社員ブログ
社員ブログ
こんにちは。建築管理部の沖見です。
今回も、前回(2022年1
 社員ブログ
社員ブログ
豊和開発株式会社 田宮といいます。私は土地有効活用の提案を行なっていますが
 社員ブログ
社員ブログ
設計監理部の三好です。今年の4月で入社して1年になります。少しずつ設計監理
 社員ブログ
社員ブログ
こんにちは。豊和開発の営業本部に所属している山本です。
土地活
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社 営業本部の石垣です。
今回のコ
 社員ブログ
社員ブログ
こんにちは。豊和開発の経営企画部の角野です。私は4月で豊和開発に入社し丸2
 社員ブログ
社員ブログ
こんにちは、豊和開発株式会社 設計監理部に所属している長浜と申します。本
 社員ブログ
社員ブログ
こんにちは。豊和開発の宮です。
当社は土地の有効活用提案を行っ
 社員ブログ
社員ブログ
豊和開発設計監理部の野田です。今回は、私たち設計監理部が建物を設計するにあ
 社員ブログ
社員ブログ
こんにちは。営業本部の佐竹と申します。土地の活用を提案する仕事上、地鎮祭に
 社員ブログ
社員ブログ
皆さん、こんにちは。
私は、豊和開発の経営企画部の岩村と申しま
 社員ブログ
社員ブログ
こんにちは。私は豊和開発の設計監理部に所属している山本と申します。
 社員ブログ
社員ブログ
皆様お久しぶりです、豊和開発株式会社【営業本部】坪田武士です。
 社員ブログ
社員ブログ
私は設計監理部に所属している大谷です。日々、介護保険施設や、児童福祉施設な
 社員ブログ
社員ブログ
こんにちは。社会人になってもうすぐ丸3年が過ぎそうな営業本部所属の黒田です
 社員ブログ
社員ブログ
建築管理部の小早川です。
過去の投稿(2021年07月17日
 社員ブログ
社員ブログ
こんにちは。私は、豊和開発株式会社で採用や総務の業務に携わっている久保と申
 社員ブログ
社員ブログ
皆さん、こんにちは2022年の9月から豊和開発でお世話になっております、営
 社員ブログ
社員ブログ
皆さんは、不動産を売却して利益を得ると発生する「譲渡所得税」を知っています
 社員ブログ
社員ブログ
こんにちは。経営企画部の村井です。
今回知ってほしい内容は『コ
 社員ブログ
社員ブログ
こんにちは、私は豊和開発株式会社の営業本部に所属している下元と申します。当
 社員ブログ
社員ブログ
こんにちは。建築管理部に所属しております沖見と申します。
私は
 社員ブログ
社員ブログ
豊和開発営業本部の田宮です。「えっ?ココって、田んぼだったんですか?」先日
 社員ブログ
社員ブログ
こんにちは、設計監理部の三好と申します。令和4年4月に豊和開発に新卒として
 社員ブログ
社員ブログ
こんにちは。豊和開発営業本部の山本です。
当社では地主様に向け
 社員ブログ
社員ブログ
こんにちは。私は豊和開発株式会社 営業本部の石垣と申します。皆さんは営業と
 社員ブログ
社員ブログ
こんにちは。私は豊和開発に入社して2年目の角野です。
私は、経
 社員ブログ
社員ブログ
豊和開発株式会社設計監理部に所属している長浜と申します。
本記
 社員ブログ
社員ブログ
こんにちは。豊和開発で営業を担当している宮と申します当社は保育施設や介護施
 社員ブログ
社員ブログ
こんにちは。私は豊和開発株式会社の設計監理部で意匠設計、設計監理を担当して
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社で設計監理部に所属している野田です。私は主にプ
 社員ブログ
社員ブログ
こんにちは、豊和開発株式会社営業本部の佐竹です。弊社は土地の有効活用を提案
 社員ブログ
社員ブログ
学生の皆さん、こんにちは。経営企画部の岩村です。
学生生活にお
 社員ブログ
社員ブログ
こんにちは。私は豊和開発の設計監理部に所属している山本と申します。
 社員ブログ
社員ブログ
豊和開発株式会社【営業本部】坪田武士です。
土地を所有している
 社員ブログ
社員ブログ
こんにちは。私は豊和開発 設計監理部の大谷です。私は設計監理部に所属し日々
 社員ブログ
社員ブログ
こんにちは。私は豊和開発に新卒で入社した、営業本部3年目の黒田です。私は学
 社員ブログ
社員ブログ
豊和開発建築管理部の小早川です。日頃から新築工事の各工程を管理する仕事に携
 社員ブログ
社員ブログ
豊和開発株式会社経営企画部 久保です。私は主に採用に関わる業務に従事してい
 社員ブログ
社員ブログ
こんにちは。営業本部の松原です。
今回のコラムは、不動産・建築
 社員ブログ
社員ブログ
こんにちは。私は豊和開発株式会社で営業本部に所属し、土地有効活用の提案営業
 社員ブログ
社員ブログ
こんにちは!豊和開発株式会社で設計監理部に所属する橋本です。
 社員ブログ
社員ブログ
こんにちは。建築管理部の沖見です。
さて、今回も引き続き堺市で
 社員ブログ
社員ブログ
経理業務を行うにあたり、法人税や所得税(源泉所得税含む)、固定資産税や自動
 社員ブログ
社員ブログ
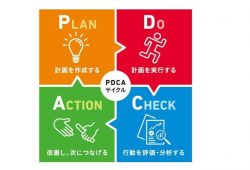
「土地活用」の目的のひとつとして、「節税対策」が上げられます。固定資産税
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社経営企画部入社2年目の角野です。
 社員ブログ
社員ブログ
こんにちは。豊和開発の宮と申します。土地の活用方法にはマンションなどの住宅
 社員ブログ
社員ブログ
豊和開発株式会社設計監理部に所属している長浜と申します。
建築
 社員ブログ
社員ブログ
こんにちは、豊和開発株式会社 経営企画部の竹川と申します。私は、入社してか
 社員ブログ
社員ブログ
こんにちは。
私は設計監理部で意匠設計、工事監理等の業務を担当
 社員ブログ
社員ブログ
こんにちは。私は豊和開発の設計監理部で建物プランの作成や確認申請、意匠設計
 社員ブログ
社員ブログ
こんにちは。豊和開発の営業本部に所属している佐竹と申します。私の父親は高知
 社員ブログ
社員ブログ
豊和開発株式会社 経営企画部の岩村です。今回は、3月よりついに始まった新卒
 社員ブログ
社員ブログ
こんにちは。私は豊和開発の設計監理部に所属している山本と申します。
 社員ブログ
社員ブログ
豊和開発株式会社営業本部の坪田です。
今回のコラムでは様々な種
 社員ブログ
社員ブログ
建築設計とは地図に残る仕事であり、その分苦労も多いですが竣工時は大きなやり
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社の黒田と申します。2020年4月に新卒社員とし
 社員ブログ
社員ブログ
建築工事現場というと、どのような景色を想像されますか?
一般的
 社員ブログ
社員ブログ
豊和開発株式会社、経営企画部の久保です。今回は当社の部署ごとの業務内容につ
 社員ブログ
社員ブログ
持っているだけでお金がかかってしまう「土地」。
図らずも相続を
 社員ブログ
社員ブログ
豊和開発株式会社で設計監理部に所属する橋本です。
私は、専門学
 社員ブログ
社員ブログ
豊和開発株式会社の下元と申します。
当社では、空地はもちろんで
 社員ブログ
社員ブログ
こんにちは。建築管理部の沖見です。
さて、今回も引き続き堺市で
 社員ブログ
社員ブログ
私は、現在豊和開発株式会社で、土地有効活用の提案を行っています。
 社員ブログ
社員ブログ
こんにちは。
私は豊和開発株式会社の設計監理部で、意匠設計と現
 社員ブログ
社員ブログ
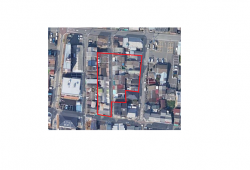
土地を数える単位に筆というものがあります。一つの例になりますが、画像の赤
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社経営企画部の角野と申します。
私は
 社員ブログ
社員ブログ
始めまして。豊和開発株式会社営業本部の佐藤です。私は今年の3月まで大学で心
 社員ブログ
社員ブログ
こんにちは、私は2021年4月に豊和開発株式会社に新卒社員として入社し、設
 社員ブログ
社員ブログ
令和5年10月1日より消費税の「インボイス制度(適格請求書等保存方式)」が
 社員ブログ
社員ブログ
近年空き家の増加が社会問題となっており、『空き家問題』という言葉をよく耳
 社員ブログ
社員ブログ
こんにちは。
私は豊和開発株式会社の設計監理部で意匠設計、工事
 社員ブログ
社員ブログ
こんにちは。私は豊和開発の設計監理部で建物プランの作成や確認申請、意匠設計
 社員ブログ
社員ブログ
豊和開発株式会社【営業本部】の坪田です。
今回のコラムでは日本
 社員ブログ
社員ブログ
私は土地活用の営業マンです。
外回りをしていると、時折見かけ
 社員ブログ
社員ブログ
初めまして!私は豊和開発株式会社 経営企画部の岩村知英と申します。この4月
 社員ブログ
社員ブログ
こんにちは、豊和開発株式会社の山本と申します。前回は、設計者やデザインに関
 社員ブログ
社員ブログ
ここ数年、介護施設が増えてきたと感じている方も多いのではないでしょうか。私
 社員ブログ
社員ブログ
こんにちは。私は豊和開発の営業本部に所属している、黒田匠太朗です。豊和開発
 社員ブログ
社員ブログ
設計監理部の大谷です。私は前回のコラムにて「新型コロナによる建築設計の変化
 社員ブログ
社員ブログ
今では少し考えられない、
1980年代後半から、1990年代初
 社員ブログ
社員ブログ
こんにちは、豊和開発株式会社 建築管理部の小早川です。
弊社で
 社員ブログ
社員ブログ
求職活動で必ず向き合わなければならない『面接』。良くないイメージを持ってい
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社 営業本部の石山です。
当社は、駐
 社員ブログ
社員ブログ
「相続税対策として土地活用が有効」という話を聞くことはありませんか?私自身
 社員ブログ
社員ブログ
こんにちは、設計監理部の橋本と申します。
以前(2020/05
 社員ブログ
社員ブログ
豊和開発で営業をしています下元と申します。当社では保育所や介護施設等の福祉
 社員ブログ
社員ブログ
こんにちは、経営企画部の竹川と申します。私は、入社してから経理業務を担当し
 社員ブログ
社員ブログ
こんにちは。建築管理部の沖見です。
今回も前回の投稿(2020
 社員ブログ
社員ブログ
特別養護老人ホームやサービス付き高齢者住宅をはじめとする、各種介護施設や保
 社員ブログ
社員ブログ
こんにちは。
私は豊和開発株式会社の設計監理部で意匠設計、確認
 社員ブログ
社員ブログ
私は、土地所有者に、土地活用のご提案を行っています。その中で、土地所有者
 社員ブログ
社員ブログ
私は、土地活用を通じていろいろな介護や福祉施設の提案を行っております。今
 社員ブログ
社員ブログ
今年も3月から22年卒向けの新卒採用活動を本格的に開始しており、学生の皆さ
 社員ブログ
社員ブログ
 社員ブログ
社員ブログ
豊和開発で経理を担当しております木村と申します。
先日、弊社役
 社員ブログ
社員ブログ
用途地域というのは、都市計画法に定められる地域地区の一つです。土地を住居系
 社員ブログ
社員ブログ
こんにちは。
私は豊和開発株式会社の設計監理部で、プランニング
 社員ブログ
社員ブログ
こんにちは。豊和開発株式会社、営業本部1年目の山副(ヤマゾエ)と申します
 社員ブログ
社員ブログ
こんにちは、豊和開発株式会社の山本と申します。今回は、建築設計者や建築デザ
 社員ブログ
社員ブログ
今回のコラムでは、土地活用と景気の関係性について書いていきたいと思います。
 社員ブログ
社員ブログ
新型コロナが猛威を振るい始めてから1年以上が経過しました。不要不急の外出
 社員ブログ
社員ブログ
こんにちは!私は2020年4月に豊和開発に新卒社員として入社し、営業本部に
 社員ブログ
社員ブログ
私は豊和開発の建築管理部に所属しており、介護施設や医療施設における新築工事
 社員ブログ
社員ブログ
企業で就業する方への転職に対する統計では、転職の経験があるとの回答が53%
 社員ブログ
社員ブログ
私が新卒採用活動をしている中で、採用担当者として数多くの学生さんとお会いし
 社員ブログ
社員ブログ
豊和開発株式会社の石山です。
当社は、駐車場等を所有しているオ
 社員ブログ
社員ブログ
コロナ渦において、3密を避けるために、就職活動をオンラインで行う企業が多く
 社員ブログ
社員ブログ
不動産業界で働く人が持っている資格に「宅地建物取引士(以下「宅建士」)」の
 社員ブログ
社員ブログ
こんにちは、豊和開発株式会社 設計監理部の橋本と申します。
建
 社員ブログ
社員ブログ
豊和開発株式会社 営業本部の下元です。
皆さんにオススメしたい
 社員ブログ
社員ブログ
こんにちは、経営企画部の竹川と申します。私は、入社して2年目で、経理として
 社員ブログ
社員ブログ
こんにちは。建築管理部の沖見です。
今回は、2020年4月10
 社員ブログ
社員ブログ
2020年も、残り僅かとなりました。今なお、終息の陰りも見えないコロナ
 社員ブログ
社員ブログ
私のお客様で、以前生産緑地を解除して有効活用された地主様がいらっしゃいまし
 社員ブログ
社員ブログ
建築でいう「外構」とは、計画建物の外部の門や塀、駐車場屋根、花壇、植栽など
 社員ブログ
社員ブログ
豊和開発株式会社の桒田(クワタ)と申します。
私は、八尾市にあ
 社員ブログ
社員ブログ
日本には離島がたくさんあります。
景色の美しい島、歴史が残る島
 社員ブログ
社員ブログ
大川に掛かる天神橋を北に渡ると、建物の間に、鳥居を模したゲートが見える。日
 社員ブログ
社員ブログ
私が新卒の採用活動をしている中で、採用担当・面接官として数多くの学生さんと
 社員ブログ
社員ブログ
豊和開発株式会社の佐竹と申します。
主に医療施設、介護施設
 社員ブログ
社員ブログ
豊和開発株式会社の営業本部で、土地資産に於ける有効活用を提案する為の営業活
 社員ブログ
社員ブログ
こんにちは、豊和開発株式会社に2020年の4月に入社した設計監理部の山本で
 社員ブログ
社員ブログ
豊和開発株式会社 営業本部新卒社員の山副(ヤマゾエ)と申します。
 社員ブログ
社員ブログ
皆様、こんにちは。
私が勤務する豊和開発株式会社は、土地有効
 社員ブログ
社員ブログ
私は、介護施設や保育園を多く設計施工している企業の設計士として保育園の設計
 社員ブログ
社員ブログ
こんにちは、豊和開発株式会社営業本部の永井と申します。私は2020年の4月
 社員ブログ
社員ブログ
豊和開発営業本部の坪田です。
当コラムでは当社がご提案する土地
 社員ブログ
社員ブログ
私は4月より豊和開発株式会社に入社した雨の日が苦手な新入社員でございます。
 社員ブログ
社員ブログ
私は、土地の有効活用を提案する企業で、クリニックなどの医療施設や、介護施設
 社員ブログ
社員ブログ
豊和開発 建築管理部の小早川です。 今回のコラムでは、私がたまたま見かけた
 社員ブログ
社員ブログ
こんにちは、豊和開発株式会社 営業本部の石山です。
当社は土地
 社員ブログ
社員ブログ
当社では、社内外への情報発信ツールとして、ホームページの他に、社報「イカす
 社員ブログ
社員ブログ
こんにちは、営業本部の松原です。
突然ですが、皆さんは「感
 社員ブログ
社員ブログ
こんにちは、設計監理部の橋本と申します。豊和開発での設計職は「
 社員ブログ
社員ブログ
豊和開発株式会社の下元と申します。
皆さんに是非オススメした
 社員ブログ
社員ブログ
皆さん「サイディング」というものご存じでしょうか。サイディングとは、建物の
 社員ブログ
社員ブログ
こんにちは。建築管理部の沖見です。
豊和開発に入社して早一年が
 社員ブログ
社員ブログ
こんにちは。経営企画部の竹川です。私は2019年に新卒として豊和開発株式会
 社員ブログ
社員ブログ
近年、地球温暖化は国際的に深刻な問題となっており、毎年猛暑・暖冬などの異常
 社員ブログ
社員ブログ
こんにちは、営業本部の松山です。私は豊和開発で土地有効活用の営
 社員ブログ
社員ブログ
こんにちは。設計監理部の高です。
今回は建築に関するおもしろい
 社員ブログ
社員ブログ
営業本部の田宮です。今私は、豊和開発で土地活用の提案を行っている毎日の中で
 社員ブログ
社員ブログ
豊和開発 経営企画部の久保です。豊和開発は、経営理念に『豊かな
 社員ブログ
社員ブログ
保育所とは、保護者が働いているなどの何らかの理由によって保育を必要とする乳
 社員ブログ
社員ブログ
今回は私が新卒の採用活動をしている中で、採用担当・面接官として数多くの学
 社員ブログ
社員ブログ
近年、異常気象や地球温暖化など建物内外の環境も変化してきており、建築にお
 社員ブログ
社員ブログ
土地の活用方法は様々で、土地それぞれに向き・不向きがあります。
 社員ブログ
社員ブログ
豊和開発 建築管理部の小早川です。当社は土地有効活用の一環として介護施設
 社員ブログ
社員ブログ
土地を所有されている方が、その土地で有効的に収益をあげるために色々な選択
 社員ブログ
社員ブログ
カラースキーム(色彩計画)とは、まとまりのある雰囲気を作るために、色のもつ
 社員ブログ
社員ブログ
 社員ブログ
社員ブログ
建築パースとは、建物の外観や室内を立体的に表現することで、平面の図面など
 社員ブログ
社員ブログ
豊和開発株式会社の下元と申します。今回は私が営業で外回りをした際に見つけ
 社員ブログ
社員ブログ
豊和開発株式会社営業本部の石山成真と申します。2019年の春に大学を卒業
 社員ブログ
社員ブログ
比較的自分の時間があると言われる学生生活ですが、勉強の他に、部活やサーク
 社員ブログ
社員ブログ
一般的に設計監理の業務内容と言えば、図面の作成やお施主様との打合せをして
 社員ブログ
社員ブログ
先日出勤中にふとまわりを見渡すと、家やマンション、商業施設、ビルなど本当に
 社員ブログ
社員ブログ
みなさま、こんにちは。
私は豊和開発株式会社営業部員の桒田(ク
 社員ブログ
社員ブログ
2019年10月25~27日の3日間、毎年恒例の社員旅行に行きました。行き
 社員ブログ
社員ブログ
豊和開発株式会社には、土地活用の提案を行う営業本部、設計業務を行う設計監理
 社員ブログ
社員ブログ
建築において構造は骨組みの部分であり、欠かすことのできないものです。今回は
 社員ブログ
社員ブログ
こんにちは。営業本部の北浦です。豊和開発に入社して、半年が経とうとしていま
 社員ブログ
社員ブログ
豊和開発がどんな事業をしていて営業職がどんな仕事をしているか等、普段の私の
 社員ブログ
社員ブログ
今回は設計活動の中で建物に関する「お金」について記事にしたいと思います。
 社員ブログ
社員ブログ
豊和開発設計監理部に新卒社員として令和元年4月に入社して早くも5ヵ月が過ぎ
 社員ブログ
社員ブログ
みなさん建築の設計業務についてご存知でしょうか?
有名な建築
 社員ブログ
社員ブログ
新たに不動産業界で就職を検討している方は多くいると思います。しかし一言で
 社員ブログ
社員ブログ
ロードサイド店舗は主に自動車での集客がメインで敷地内に駐車場を設置してお
 社員ブログ
社員ブログ
当社は名刺に、CMキャラクターである『イカす侍』を入れている。営業現場で
 社員ブログ
社員ブログ
今回は私が
 社員ブログ
社員ブログ
いつもご覧いただきありがとうございます。経営企画部の岡田です。10月27日
 社員ブログ
社員ブログ
企画建設本部の橋本です。今回は私の地元である、兵庫県の姫路市にある姫路城の
 社員ブログ
社員ブログ
企画建設本部の久保です。
今回で19回目の投稿となります。香
 社員ブログ
社員ブログ
豊和開発の徳村です。年末年始休暇に1泊2日で岐阜県にスキーに行ってきました
 社員ブログ
社員ブログ
皆様お久しぶりです。営業本部の坪田です。今回の投稿は豊和開発で
 社員ブログ
社員ブログ
企画建設本部 設計監理部の奥村です。すでに約1ヶ月を経ようとしていますが、
 社員ブログ
社員ブログ
豊和開発の徳村です。最近は神戸市を営業に回っていますので、今回
 社員ブログ
社員ブログ
宮城県仙台市で設計監理に携わらせて頂いた、特別養護老人ホームの「リズムタウ
 社員ブログ
社員ブログ
経営企画部の岡田です。今回は、先日の弊社社員が出演したラジオに
 社員ブログ
社員ブログ
いつもご覧いただきありがとうございます。
 社員ブログ
社員ブログ
突然ですが皆様ネパールという国をご存知ですか?私は国名は知って
 社員ブログ
社員ブログ




